研究 (Research)
最終更新日:
ジャミングの物理における普遍性 (Universality in the physics of jamming)
准教授 吉野 元(サイバーメディアセンター) YOSHINO Hajime(Cybermedia Center)
研究の概要
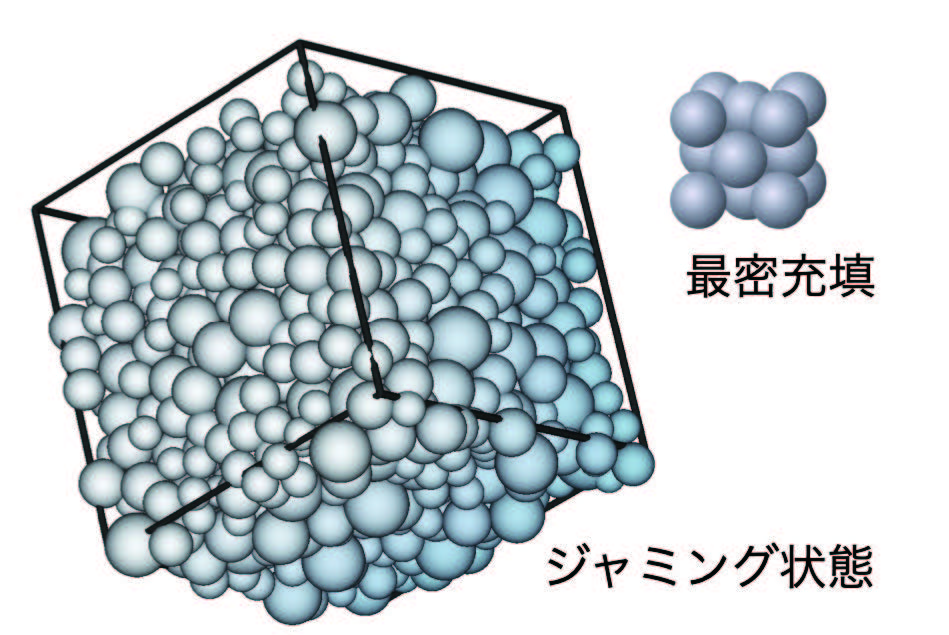
最もシンプルなガラス状態である剛体球ガラスに対して、圧縮やシア(剪断)をかける数値シミュレーションをスーパーコンピューター用いて行いました。その結果、様々な密度と異方性をもつ膨大な数のジャミング状態を生成することに成功しました(図1)。これらのジャミング状態について解析すると、力学的にマージナルな安定状態であり、すべて同一の臨界性を持つことが明らかになりました。例えば、粒子の中心から距離rにある他の粒子の平均的な数(図2)を見ると、様々なジャミング密度φjを持つ配置で共通する普遍的な振る舞いになっています。左図から平均配位数は6であり、力学的にぎりぎりの安定状態にあることがわかります。また右図から、ほとんど接触しかけている粒子の数は、普遍的な指数で特徴づけられるベキ分布に従っていることがわかります。これはある種の臨界状態にあることを示唆します。本研究の成果により、身近にありながら結晶に比べて多くの未解決問題をもつガラスの基礎物理の理解が進展すると期待されます。

研究の背景と結果
球を最も密に箱に詰める方法(最密充填)は、古くから議論されていました。17世紀にJ. ケプラーが3次元での最密充填は「面心立方格子」であると予想し、400年ほど後の1998年になってトーマス・C・ヘイルズがこれを証明しました。最密充填の密度は、体積分率で測って0.74048…です。これに対し、「でたらめに」球を詰める実験をJ.ベナールとJ.メイソンらが1960年に行い (J. Bernal, J. Mason, Nature 188 (4754), 910 (1960))、密度0.64付近でジャミング、すなわちこれ以上詰められない、の状態が得られることを見出しました。彼らはこれを「ランダム最密充填」と呼びました。しかし、その後の研究で、ランダムに詰めたジャミング状態は、圧縮を始める前の初期状態の作り方などによって様々な密度のものが得られることがわかってきていました。ジャミングはマヨネーズや歯磨き粉など高密度のソフトマターの力学的性質を支配する重要な現象です。
本研究グループでは、圧縮だけでなく、体積一定のまま箱を変形させるシア(剪断)によっても様々なジャミング状態が得られることを、スーパーコンピューターを用いた剛体球ガラスの大規模数値シミュレーションで見出しました。この現象は、粒子間に摩擦がある場合には知られていましたが、摩擦がなくても実現することが初めて示されました。さらに圧縮とシアを組み合わせて得られる様々な密度のジャミングがすべて共通した性質を持っていること、すなわち、これら全てが力学的にぎりぎりの安定性をもつ平均配位数6の状態にあること(図2左)、様々な物理量が共通した臨界現象を示すこと(図2右)を明らかにしました。最密充填の場合、配位数は12で、構造としては一つしかなく、力学的には安定であることときわめて対照的です。
研究の意義と将来展望
本研究成果により、結晶とは異なり、乱れたまま固体となったガラスの基礎的理解が進むことが期待されます。また将来的には、身近な工業材料や食品において重要なコロイドなど、高密度のソフトマターの制御に役立つと期待されます。
担当研究者
准教授 吉野 元(サイバーメディアセンター)
キーワード
統計力学/ソフトマター物理/ガラス転移/ジャミング
応用分野
レオロジー/アモルファス物質
